一文带你从欧拉角的角度搞懂左手坐标系到右手坐标系的转换

作者：StubbornHuang
时间：2019年11月30日凌晨0点30分
注意：码字不易，如果需要转载请注明作者名称以及转载链接。

来到这个专栏比较干货的一篇文章，我们如何正确的理解从左手坐标系到右手坐标系的转换，没有复杂的矩阵变换，没有难以理解的四元数计算，而是使用更加直观的欧拉角陈述一下左手坐标系到右手坐标系转换的合理思路。

1 转换示例

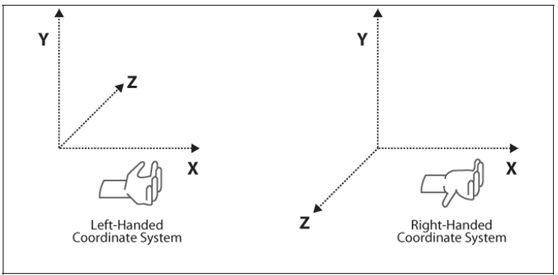
我们以上图为示例，考虑从Yup左手坐标系到Yup右手坐标系的变换，左侧图为Yup左手坐标系，下文以A坐标系表示，右侧图为Yup右手坐标系，下文以B坐标系表示。

如果我们有一个物体（命名为Object）在左手坐标系中的世界坐标为（Ax,Ay,Az），其旋转用欧拉角表示为（Aeulerx,Aeulery,Aeulerz），那么我们如何在右手坐标系B中以相同的位置和相同的旋转表示该物体呢？能够在右手坐标系B中以相同的位置以及旋转放置该物体其同等的意义就是可以正确的进行左手坐标系A到右手坐标系B的转换，这种转换既包括位移同时也包括旋转。

2 从左手坐标系A到右手坐标系B位移的正确转换

如上一节所述，物体Object在左手坐标系的位置为（Ax,Ay,Az），那么在右手坐标系B中的如何正确的表示呢？

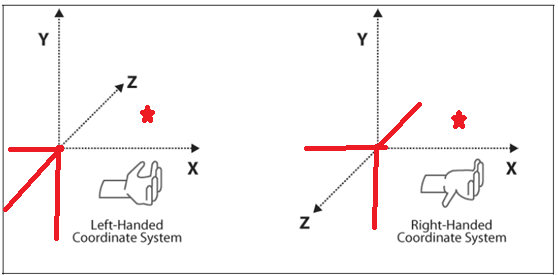
我们仔细观察第一节中的左右坐标系的朝向，我们可以很简单的发现，A坐标系的Y轴的正向与B坐标系Y轴的正向一致，A坐标系的X轴的正向朝向与B坐标系X轴的正向一致，A坐标系的Z轴的正向与B坐标系Z轴的正向相反，如果物体Object在坐标系A的摆放位置为（Ax,Ay,Az），那么显而易见，物体Object对应在坐标系B的位置为（Ax,Ay,-Az），如下图所示。

3 从左手坐标系A到右手坐标系B旋转的正确转换

好了，经过上一节，我们会发现，左右手坐标系中位置的转换是比较简单的，这也是很多人容易理解的。谷歌百度大部分的博客以及论坛上面的文章对位置变换的介绍也是非常的一致，说的也比较浅显易懂，但是它们在说明旋转在左右坐标系变换的时候，我的天呐，看的头疼(也许是我太垃圾了)。有从矩阵变换的角度去说明这个问题的，也有人总结什么改变四元数的正负值以及交换位置的简单方法的，我一个都没有看懂，更多的是觉得莫名奇妙，因为没有一个人能够浅显易懂的说明这个问题。

那么回到正题上，如何将物体Object在左手坐标系A的旋转正确的转换到右手坐标系B中呢？

我们先详细介绍一下欧拉角的含义，在专栏的前几篇文章我已经重点介绍过了，正常情况下，在左手坐标系中，绕轴的旋转正方向为顺时针方向，而在右手坐标系中，绕轴的旋转正方向为逆时针方向。另外欧拉角的大致定义为：
（1）pitch角：表示物体上下旋转，飞机抬头低头；
（2）Yaw角：表示物体左右偏；
（3）Roll角：表示物体侧翻；
一般的，欧拉角的旋转顺序都为Pitch-Yaw-Roll的顺序。
那么在左手坐标系A中，pitch角为绕X轴旋转，Yaw角为绕Y轴旋转，Roll角为绕Z轴旋转，那么左手坐标系A的欧拉角的旋转顺序为XYZ，旋转正向为顺时针旋转。
而在右手坐标系B中，pitch角为绕X轴旋转，Yaw角为绕Y轴旋转，Roll角为绕Z轴旋转，那么右手坐标系B的欧拉角的旋转顺序为XYZ，旋转正向为逆时针旋转。

那么如何将A在左手坐标系A中旋转欧拉角表示到右手坐标系中呢？

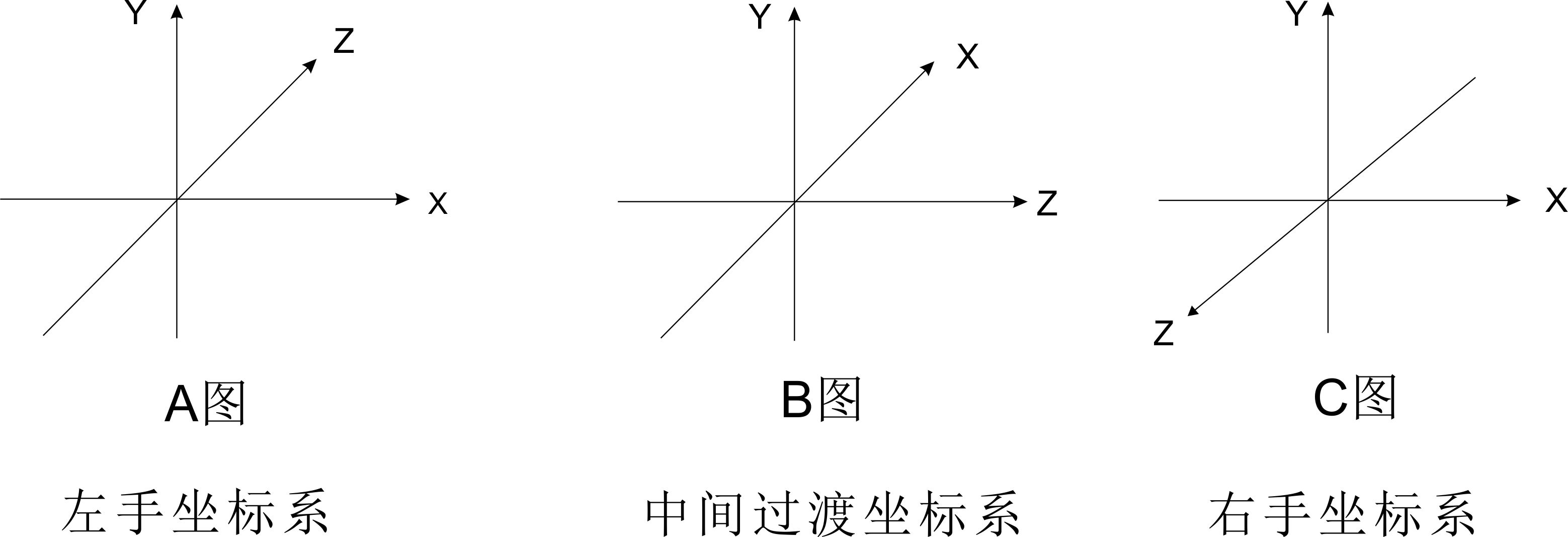
我们引入一个中间过渡坐标系来浅显的说明这个问题，如下图所示：

如上图所示，左手坐标系A如A图所示，右手坐标系B如C图所示，即我们想要我们转换的目标坐标系，我们在A和B之间增加一个过渡坐标系（如B图所示），该坐标系同样为右手坐标系，但是该坐标系与坐标系A所有轴的正方向保持一致，将该过渡坐标系记为C坐标系。

注意：我们将旋转从左手坐标系A转换到右手坐标系B中的问题转换为先将左手坐标系A转换到过渡的右手坐标系B,然后再将B坐标系转换到目标坐标系C中。

3.1 旋转从左手坐标系A转换到过渡右手坐标系C中

需要说明的是，过渡坐标系C的旋转顺序为，ZYX，旋转正方向为逆时针方向。

如果该物体Object在左手坐标系A中的旋转表示为欧拉角，其中pitch角为eulerx,Yaw角为eulery,Roll角为eulerz,那么该物体在左手坐标系A中绕X轴旋转了eulerx度，绕Y轴旋转了eulery度，绕Z轴旋转了eulerz度，该旋转通过欧拉角表示为（eulerx,eulery,eulerz）。

（1）物体Object在左手坐标系A中绕X轴旋转了eulerx度，在考虑旋转正向的情况下，相当于在过渡右手坐标系C中绕Z轴旋转了-eulerx度；
（2）物体Object在左手坐标系A中绕Y轴旋转了eulery度，在考虑旋转正向的情况下，相当于在过渡右手坐标系C中绕Y轴旋转了-eulery度；
（3）物体Object在左手坐标系A中绕Z轴旋转了eulerz度，在考虑旋转正向的情况下，相当于在过渡右手坐标系C中绕X轴旋转了-eulerz度；

所以在上述概念的基础上，由左手坐标系A向中间过渡坐标系C旋转可以参照以下伪代码，

其中四元数类Quat右,三维向量类Vec右均为在右手坐标系中使用的数学类，A.eulerX，A.eulerY,A.eulerZ为在左手坐标系A中的欧拉角。为避免欧拉角万向锁问题，中间采用四元数进行计算。

float rad = 0.0174532925199444;
Quat右 qx(Vec右(1,0,0), -A.eulerZ*rad);   // 得出在中间过渡坐标系C中绕X轴的旋转四元数
Quat右 qy(Vec右(0,1,0), -A.eulerY*rad);  // 得出在中间过渡坐标系C中绕Y轴的旋转四元数
Quat右 qz(Vec右(0,0,1), -A.eulerX*rad);  //  得出在中间过渡坐标系C中绕Z轴的旋转四元数

// 中间过渡坐标系的旋转顺序为ZYX，则中间过渡坐标系的计算结果如下：
Quat右 q = qz * qy * qx;

3.2 从过渡右手坐标系C转换到目标右手坐标系B

然后从中间过渡坐标系转换到右手坐标系，即绕Y轴顺时针旋转90度，而在右手坐标系中，逆时针旋转为旋转正向，即

Quat右 qSecond(Vec右(0,1,0),-90*rad); // 绕Y轴顺时针旋转90度。

Quat右 result = q * qSecond; 

则最后的四元数result，则为从左手坐标系到右手坐标系需要进行的旋转变换。

4 总结

我也不知道我有没有阐述明白，我觉得应该比较容易懂了，相比于其他的文章而言。
我已经使用这套理论做了正确的Unity到UnrealEngine的互相转换。
其他各种类型的坐标系的转换可以使用相同的理论进行推广。
有任何疑问，可以留言，或者到CSDN-HW140701发私信询问，或者直接发送邮件到stubbornhuang@qq.com。